La Paz. Machine Learning. Segunda edición. 2020

Introducción

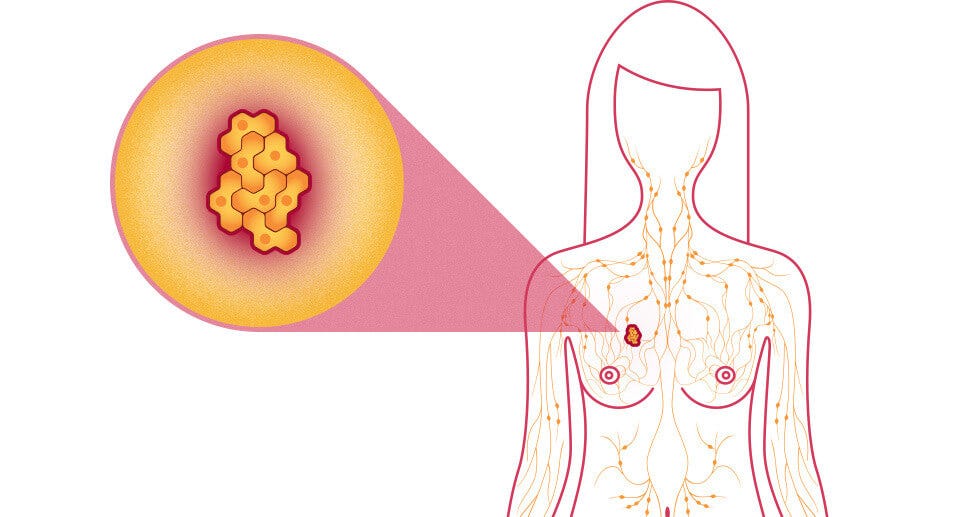
El cáncer de mama es la primera causa de muerte por tumores malignos en las mujeres a nivel mundial. Al menos en el año 2019 murieron cerca de 688 mil debido este padecimiento, lo cual nos da una tasa de mortalidad para mujeres mayores de 20 años de 24.7 por cada 100 mil.

Motivación

Existe una brecha de mortalidad por cáncer de mama entre países por nivel de ingresos, el 70%(483,000) de los fallecimientos ocurren en los países de ingresos medios y bajos. ¿A qué se deberá?, sucede que en los países de ingresos medios y bajos, hay una falta de acceso a servicios de diagnóstico y tratamiento de esta enfermedad.

Tasa de mortalidad e incidencia

1. Norteamérica 22%
2. Latinoamérica y el Caribe 38%
3. África Sub-Sahariana 65%

Entre el 50 y 63% de las muertes por cáncer de mama en todo el mundo son prevenibles con detección temprana y tratamiento adecuado. Entre el 66 y 74% de estas muertes que son prevenibles ocurren en países en desarrollo. Asimismo, el cáncer de mama, detectado a tiempo y con tratamiento adecuado puede curarse. Y en caso de que no, puede elevar la calidad de vida de las pacientes al menos hasta 5 años (en Norteamérica).

De esta problemática surge nuestro proyecto social. Sabemos que la situación es muy desfavorable para las mujeres, así que podemos contribuir a generar un modelo de machine learning que pueda ayudar a la predicción de este tipo de tumores con el cual, en un futuro muchas mujeres podrían acceder a un método de detección barato y digno, aumentando así su calidad de vida al enfrentarse con esta enfermedad genética.

Objetivo

Explorar distintos algoritmos de ML (Machine Learning, por sus siglas en inglés) supervisados y no supervisados utilizando el dataset de Wisconsin sobre diagnóstico (explicado más adelante), para compararlos y verificar cual es el que nos proporciona el mejor modelo de detección de cáncer de mama, así como revisar que variables proporcionan mayor información sobre la detección.

Como objetivo sería plantear una generalización de base de datos que pudiera implementarse en cualquier país al que se lleve este diagnóstico.

Proyecto

Se trabajó en una comparativa de ciertos modelos supervisados y no supervisados para determinar la precisión de cada uno y posteriormente utilizarlo para la predicción.

Dataset

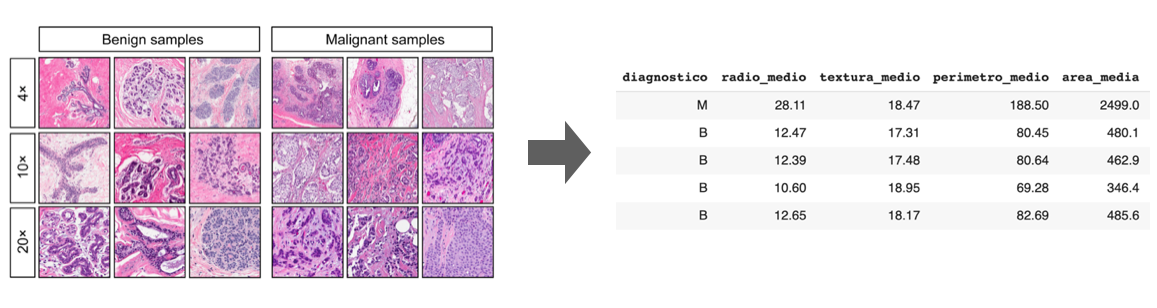
Los datos que vamos a utilizar para este primer ejercicio son los proporcionados en el dataset de diagnóstico de Wisconsin que contiene variables sobre la forma del tumor (en términos de núcleo de las células) y su dianóstico, como se muestra a continuación:

1. id: etiqueta por observación.
2. diagnóstico: variable binaria que clasifica el tumor. (M=maligno, B=benigno)
3. radio: media de las distancias del centro al perímetro.
4. textura: desviación estándar de los valores gradiente de las imágenes.
5. perímetro: medida del contorno del núcleo celular.
6. área: medida del área del núcleo celular.
7. suavidad: variación local de las longitudes del radio
8. compacidad: medida calculada por ((perímetro²/area) -1)
9. concavidad: severidad de las porciones cóncavas del contorno
10. puntos de concavidad: número de las porciones cóncavas del contorno
11. simetría: similitud entre partes con respecto a ejes.
12. dimensión fractal: índice comparativo sobre el detalle de un patrón observado de células.

De las variables 3–12 asociamos las métricas: media, error estándar, error extremo.

Análisis exploratorio

Después de haber revisado las variables del dataset procedemos a evaular la distribución del feature diagnostico para saber el balanceo de los datos, esto tiene una repercusión a la hora de entrenar a los modelos, porque como podemos ver en la gráfica siguiente tiene una mayor cantidad de datos asociada a diagnóstico de tumores benignos.

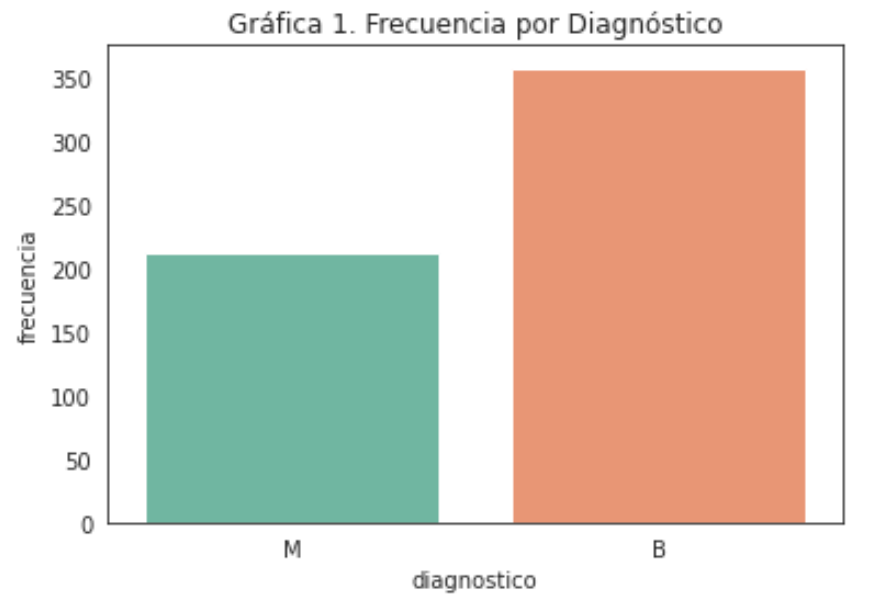
Posteriormente procederemos a ver los mapas de correlaciones entre variables para identificar si hay que hacer algún preprocesamiento antes de entrenar los modelos.

Las gráficas anteriores ilustran que en general los tres mapas muestran correlaciones similares, los promedios muestran una correlación más intensa que los valores extremos y a su vez, los valores extremos muestran una correlación más clara que el error estándar, sin embargo en los tres mapas se mantiene la tendencia entre variables.

Destacaremos las correlaciones más evidentes:

1. radio con perimetro/área/puntos de concavidad: se debe a la forma de calcular estas variables dependen directamente del radio.
2. perímetro con área/ concavidad/puntos de concavidad: estas correlaciones tienen que ver con lo mencionado en el 1.
3. suavidad con compacidad
4. compacidad con concavidad/puntos de concavidad/simetria

Después se realizaron los mapas de correlaciones más específicos que incluyen las tres métricas de las variables con relaciones más destacadas mencionadas anteriormente.

La siguiente gráfica tiene una particularidad, se observa que para las métricas del área los extremos están altamente correlacionados con la media. Y el error estándar es la métrica menos correlacionada con respecto a las otras dos.

Por último mostraremos las distribuciones y diagramas de dispersión para la media por el tipo de diagnostico, lo cual nos da un indicador de como se comportan las densidades que se puede englobar en los siguientes grupos:

1. Existe una separación casi total entre densidades: no comparten ni forma ni soporte.
2. Existe una separación regular entre densidades: comparten forma o soporte.
3. Existe una separación mínima entre densidades: comparten forma y soporte excepto ligeras variaciones.

Algoritmos no supervisados

PCA

Proponemos este análisis debido a que la estructura de nuestra base de datos tiene una dimensión alta (30 variables) por lo tanto esta técnica de análisis no supervisado nos ayudará a reducir la cantidad de componentes (variables) de nuestra base de datos, proyectando las variables originales a un subconjunto de las mismas.

El conjunto final de las variables escenciales después de este análisis, eliminará las que estén posiblemente correlacionadas. Tenemos ahora una aproximación apriori que terminará de definirse con este análisis, dado que queremos formar dos clusters por la forma binaria que tiene nuestra variable objetivo diagnostico.

La siguiente tabla muestra el porcentaje de varianza que acumula cada una de las componentes principales, consideramos en principio 10 componentes principales, como se observa en la tabla la primera y segunda componente explican el 44.27% y el 18.97% de la varianza respectivamente, lo que implica que las primeras dos componentes explican el 63.24% de la varianza.

Así que repetiremos el procedimiento pero para ahora solo sacar 2 componentes, ya que obtienen más del 60% de la varianza total.

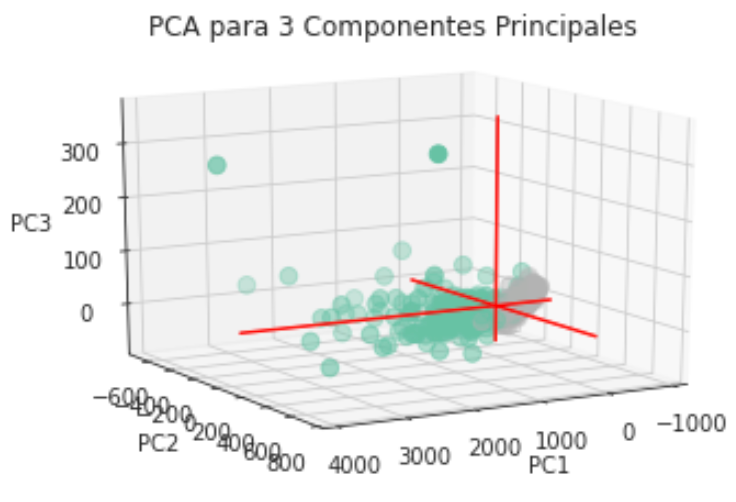
Ahora vamos a intentarlo con n=3 y podremos observar el mismo comportamiento que con dos dimensiones. En conclusión hay un agrupamiento claro con respecto al tipo de diagnóstico, incluso podría separarse linealmente (con una recta en el caso bidimensional y con un plano en el caso tridimensional) salvo algunas observaciones que se diseminan por completo.

K-Means

Para este algoritmo de ML, utilizamos el dataset sin reducción, y entrenamos el modelo para que realizara una maximización de la separación de los clústers dadas las características que tenemos (28 variables, removiendo el label).

Para este caso una visualización tipo silueta puede ayudar mucho a explicar los resultados. El Silhouetter Score fue de 0.697 es decir, que tan bien separados están los clústers, recordando que 0 quiere decir que hay overlapping y 1 que están perfectamente delimitados.

Para probar este modelo decidimos generar datos random con las variables seleccionadas del dataframe y estos fueron los resultados:

El modelo es capaz de clasificar si están en 1 (Benigno) y 0 (Maligno) dependiendo de los valores entrantes que fueron generados de manera random. Esto posteriormente con datos reales, podría detectar tumores de mama hasta con una probabilidad de 69%, lo cual es poco deseable. Más adelante con los algoritmos supervisados podremos elevar este porcentaje.

Algoritmos Supervisados

Regresión Logística

Nuestro proyecto entra en la categoría de clasificación binaria, debido a que tenemos una variable diagnostico que solo nos muestra si es benigno o maligno. Por tanto, este modelo nos beneficia al darnos una primera aproximación para la resolución del problema. En primera instancia, aplicamos el algoritmo de regresión logística para los datos en sus 30 dimensiones y para ver claramente como está funcionando este clasificador, emplearemos una matriz de confusión como se muestra a continuación.

Dada la predicción anterior podemos incluir la precisión del modelo calculada con la métrica de sklearn accuracy_score fue de 0.962765. Resultado que es mucho mejor que nuestro anterior modelo no supervisado (KMeans).

Un diagnóstico más específico es la probabilidad de predicción por observación, es decir, qué tan probable es que esa observación sea clasificada como Benigno o Maligno. Así que vamos a ver su desempeño por cross-validation. Cross-Validation Accuracy Scores [0.94871795 0.92105263 0.94736842 0.92105263 0.97368421 0.97368421 0.97368421 0.94736842 0.92105263 0.94736842].

Por lo anterior concluimos que en promedio tenemos una precisión del 94.6%, sin embargo es necesario revisar la estructura del modelo y los supuestos del mismo.

Regresión Logística paso por paso

Después de la pasada primera aproximación del modelo es momento de revisar si se cumplen ciertos supuestos requeridos para el desarrollo de la regresión logística, algunos de estos supuestos los enunciaremos a continuación.

1. La variable objetivo debe ser binaria. En nuestro caso diagnostico es ‘M’ o ‘B’.
2. El resultado de la variable de interés asociado al “éxito” debe ser 1.
3. Solo deben incluirse las variables significativas.
4. Las variables deben ser independientes entre sí, para evitar el problema de multicolinealidad.
5. Debe haber un tamaño de muestra “suficiente”

Procederemos a la construcción de la regresión lineal cuidando estos supuestos.

En un principio detectamos que nuestra muestra no estaba balanceada en cantidad de observaciones malignas (~37%) y benignas (~62%), para lo cual se utilizó la biblioteca SMOTE debido a que realiza una generación aleatoria de las observaciones faltantes basada en KNN.

Nota: Solo sobremuestreamos en el conjunto de datos de entrenamiento, puesto que la información que hay en los datos de prueba no será incorporada en el modelo de entrenamiento.

Para “Solo deben incluirse las variables significativas”, es necesario identificar las variables que tengan el mejor rendimiento, así poder incluir finalmente variables o características más pequeñas y más representativas. Estas fueron las variables elegidas:

“radio_medio”,”textura_medio”,”perimetro_medio”,”area_media”,”suavidad_media”,”compacidad_media”,”concavidad_media”,”puntos_concavidad_media”,”simetria_media”,”dim_fractal_media”,”radio_ee”,”textura_ee”,”perimetro_ee”,”area_ee”,”suavidad_ee”,”compacidad_ee”,”concavidad_ee”,”puntos_concavidad_ee”,”simetria_ee”,”dim_fractal_ee”,”radio_extremo”,”textura_extremo”,”perimetro_extremo”,”area_extremo”,”suavidad_extremo”,”compacidad_extremo”,”concavidad_extremo”,”puntos_concavidad_extremo”,”simetria_extremo”,”dim_fractal_extremo”

Ahora implementaremos el modelo con las nuevas variables seleccionadas y los datos balanceados:

Verificando manualmente el valor p de cada una de las variables, quitamos aquellas tales que el valor p exceda .05 que es nuestro nivel de confianza. Ahora vamos a revisar el supuesto de independencia revisaremos nuevamente las correlaciones con las variables finales de nuestro modelo.

El mapa de correlaciones anterior sugiere una alta correlación para radio_medio y perimetro_extremo por lo que quitaremos una de las dos basándonos en la calificación obtenida en el desempeño del modelo.

Ahora las variables seleccionadas muestran una correlación en general baja, lo que aporta a la hipótesis de independencia. Ahora calificaremos nuevamente el desempeño de nuestro modelo. Primero obtendremos la nueva matriz de confusión y posteriormente la precisión.

Ahora nuestra precisión es de 0.918. Así se ve la matriz de confusión:

Por último, vamos a comprobar con un ROC Curve que es una herramienta usada en modelos de clasificación binarios, la forma de interpretar esta gráfica es que un clasificador preciso debe estar lo más lejos de la línea identidad (excepto en los extremos).

Después de este procesamiento, podemos concluir que tenemos una precisión del 92% en promedio la cual es inferior a la propuesta en el primer modelo de regresión logística, la ventaja de este último modelo es la reducción de dimensión de 30 variables a 6 además de que se apega más a los supuestos del modelo de Regresión Logística, esto puede tener implicaciones en cuanto a generalización (que funcione en otras bases de datos) y costo computacional (menos tiempo de procesamiento).

SVM

Este algoritmo tiene como objetivo clasificar con base en distancias a hiperplanos diferentes clases de observaciones, es preferido por su nivel de precisión y su bajo costo computacional. Además otra ventaja de este algoritmo es que funciona bien para grandes dimensiones, es decir para gran cantidad de variables explicativas.

Después de esta implementación obtuvimos una precisión del 92.98% sin embargo, hay ciertas observaciones que es importante resaltar sobre este algoritmo.

• Este algoritmo no es muy preciso cuando no hay una clara separación entre las clases de variables, en nuestro caso puede observarse en la visualización de PCA que existen observaciones que están mezcladas entre clases.
• Este algoritmo optimiza distancias, es decir que no existe un fundamento estadístico para la clasificación, no considera la distribución de los datos.

KNN

Implementaremos ahora el algoritmo de KNN que es un algoritmo no paramétrico usado con frecuencia como modelo de clasificación o regresión.

Primero graficaremos el número de clústers que maximiza la función.

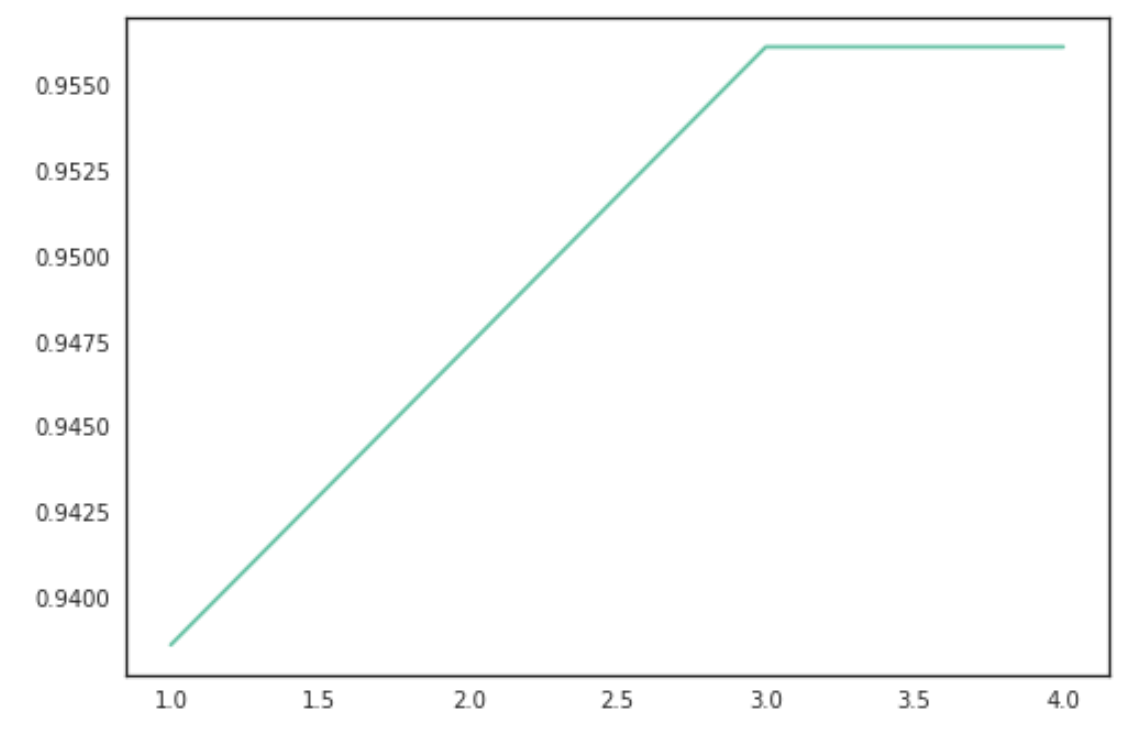
Obtuvimos una precisión del 96.27% que es mayor a las precisiones obtenidas en los modelos anteriores, sin embargo hay que hacer ciertas observaciones sobre este modelo:

• Este modelo no tiene un buen desempeño cuando hay gran cantidad de variables. Esto implica que para un nivel de precisión fijo, conforme crece el número de variables explicativas la cantidad de observaciones debe crecer de manera exponencial.
• Tiene poco poder de generalización, es decir, tiene problemas de sobreajuste.
• Los puntos anteriores implican que existe un gran costo computacional correr este algoritmo.

And last but not least…

Random Forest

Como esperábamos este modelo tiene una precisión del 97.36% que es la más alta con respecto a los demás modelos, algunos comentarios sobre este modelo son:

• Este modelo es fundamentalmente predictivo, no explicativo, no tiene un sentido claro del procesamiento de información.
• Para problemas complejos el costo computacional puede crecer demasiado.

Conclusiones

Después de probar los modelos anteriores notamos que cada una de las implementaciones tienen ventajas y desventajas, además existen modelos que se complementan entre sí como observamos en el caso de PCA, regresión logística y SVM, en donde un modelo de aprendizaje no supervisado puede trazar las posibilidades de clasificación y reducción de dimensiones, posteriormente implementar un modelo de aprendizaje supervisado para la predicción de la variable dependiente.

Cada problema tiene un contexto particular que debe ser considerado para la propuesta de modelos específicos, la cantidad y tipo de variables explicativas configuran el marco de referencia para la implementación de modelos.

En el caso particular de nuestro problema, el objetivo de predicción de la variable dependiente diagnóstico puede ser abordado en general desde dos perspectivas:

• Por un lado, tenemos la meta de pronósticar con la mayor precisión si el diagnóstico para la paciente es favorable o lamentablemente desfavorable, de acuerdo a las métricas obtenidas si seguimos esta única meta el modelo de Regresión Logística nos da una precisión superior a los demás lo que se traduce en un error mínimo al clasificar, sin embargo es cuestionable su generalización a otras bases de datos relacionadas con este problema.
• Por otro lado, tenemos la meta de generalizar este modelo a otras bases de datos, por lo que en este sentido nos inclinamos por el modelo de Regresión Logística paso a paso, dado que además de que se apega mejor a los supuestos específicos del modelo disminuye la dimensión del problema de 30 variables explicativas a 6 varaiables, esto último tiene impacto positivo en términos de procesamiento computacional y almacenamiento/recolección de datos.

Es cierto que para el objetivo de generalización perdemos puntos porcentuales de precisión (dado que la Regresión Logística paso a paso tiene una precisión del 92% en promedio) pero la ventaja de generalizar este modelo es una prioridad específicamente dadas las cifras de mortalidad que actualmente están asociadas al cáncer de mama.

Extender este modelo a bases de datos generadas por otros países, especialmente los de menor ingreso y peor cobertura de salud pública se traduce en menores tiempos de espera en diagnóstico, menor costo de procedimientos y tratamiento oportuno para las pacientes.

Otra ventaja en términos prácticos que sigue el mismo eje, es que las variables relevantes incluídas en el modelo final son 6, lo que representa una disminución del 80% en la dimensión del problema, para los países con menor presupuesto para investigación y salud será más barato crear bases de datos con solo 6 métricas por observación, también el almacenamiento y el posterior procesamiento de la información será más fácil y oportuno.

Referencias

Los datos presentados en la introducción fueron obtenidos de los siguientes artículos:

• http://tomateloapecho.org.mx/Pdfs/Numeralias/2020/FS%20CAMA%20ESP%20(09-20).pdf
• http://tomateloapecho.org.mx/Pdfs/Numeralias/2019/Numeralia%20MEX-MUNDO%202019.pdf
• http://tomateloapecho.org.mx/Pdfs/Numeralias/2016/Cancer%20de%20mama%20y%20mujeres%20jovenes%20en%20America%20Latina%20y%20el%20Caribe.pdf
• https://www.aprendemachinelearning.com/k-means-en-python-paso-a-paso/
• https://rstudio-pubs-static.s3.amazonaws.com/344010_1f4d6691092d4544bfbddb092e7223d2.html

Integrantes

• María José Sedano Castañeda
• Dante Fernando Bazaldua Huerta
• Carlos Alberto Gomez Vazquez

Presentación del proyecto: DemoDay

Repositorio

En el siguiente repositorio se encuentra el código usado para desarrollar esta aplicación: https://github.com/SaturdaysAI/Projects/tree/master/Lapaz/2021.ML2/Equipo%204

¡Más inteligencia artificial!

La misión de Saturdays.ai es hacer la inteligencia artificial más accesible (#ai4all) mediante cursos y programas intensivos donde se realizan proyectos para el bien (#ai4good).

Infórmate de nuestro master sobre inteligencia artifical en https://saturdays.ai/master-ia-online/

Si quieres aprender más inteligencia artificial únete a nuestra comunidad en community.saturdays.ai o visítanos en nuestra web www.saturdays.ai ¡te esperamos!